 A palavra probabilidade deriva do Latim probare (provar ou testar). Informalmente, provável é uma das muitas palavras utilizadas para eventos incertos ou conhecidos, sendo também substituída por algumas palavras como “sorte”, “risco”, “azar”, “incerteza”, “duvidoso”, dependendo do contexto.
A palavra probabilidade deriva do Latim probare (provar ou testar). Informalmente, provável é uma das muitas palavras utilizadas para eventos incertos ou conhecidos, sendo também substituída por algumas palavras como “sorte”, “risco”, “azar”, “incerteza”, “duvidoso”, dependendo do contexto.
A probabilidade é um número que varia de 0 (zero) a 1 (um) e que mede a chance de ocorrência de um determinado resultado. Quanto mais próxima de zero for a probabilidade, menores são as chances de ocorrer o resultado e quanto mais próxima de um for a probabilidade, maiores são as chances.
As probabilidades podem ser expressas de diversas maneiras, inclusive decimais, frações e percentagens. Por exemplo, a chance de ocorrência de um determinado evento pode ser expressa como 10%; 5 em 10; 0,20 ou 1/7.
EXPERIMENTO ALEATÓRIO
Experimento é qualquer atividade realizada que pode apresentar diferentes resultados. Um experimento é dito aleatório quando não conseguimos afirmar o resultado que será obtido antes de realizar o experimento. Um experimento é dito equiprovável se todos os possíveis resultados possuem a mesma chance de ocorrer.
ESPAÇO AMOSTRAL E EVENTO
Em uma tentativa com um número limitado de resultados, todos com chances iguais, devemos considerar:
ESPAÇO AMOSTRAL (E)
Espaço amostral é o conjunto E cujos elementos são todos os possíveis resultados que podem ser obtidos na realização de um experimento.
EVENTO (A)
Evento é qualquer subconjunto de um espaço amostral.
CÁLCULO DE PROBABILIDADES
Seja um evento A de um espaço amostral referente a um experimento aleatório e equiprovável.
A probabilidade P(A) de se obter o evento A é dada por:
Onde:
- n(A) é o número de elementos do evento A;
- n(E) é o número de elementos do espaço amostral
ESTATÍSTICA
A Estatística está presente em todas as áreas da ciência que envolvam o planejamento do experimento, a construção de modelos, a coleta, o processamento e a análise de dados e sua consequente transformação em informação, para validar hipóteses científicas sobre um fenômeno observável. Desta forma, a Estatística pode ser pensada como a ciência de aprendizagem a partir de dados.
A aplicação de técnicas estatísticas a dados meteorológicos tem a vantagem de compactar o enorme volume de dados, medidos, por exemplo, em uma estação, em uma simples tabela ou uma equação, capaz de sumariar todas as informações de modo a facilitar as inferências sobre os dados.
DEFINIÇÃO
A estatística é uma coleção de métodos para planejar experimentos, obter dados e organiza-los, resumi-los, analisá-los, interpretá-los e deles extrair conclusões.
NOÇÕES DE ESTATÍSTICA
AMOSTRA
São elementos coletados dentro do vasto universo.
ROL
É toda sequência de dados numéricos.
Exemplo:
Os cincos alunos de uma amostra apresentaram as seguintes notas na prova bimestral de matemática 6; 4; 8; 7; 8. Apresentando esses dados em rol, temos: (4; 6; 7; 8; 8) ou (8; 8; 7; 6; 4).
CLASSES
Qualquer intervalo real que contenha um rol da amostra.
MEDIDAS DE POSIÇÃO
São as estatísticas que representam uma série de dados orientando-nos quanto à posição da distribuição em relação ao eixo horizontal do gráfico da curva de frequência.
As medidas de posições mais importantes são as medidas de tendência central ou pro médias (verifica-se uma tendência dos dados observados a se agruparem em torno dos valores centrais).
As medidas de tendência central mais utilizadas são: média aritmética, moda e mediana.
MÉDIA ARITMÉTICA
É igual ao quociente entre a soma dos valores do conjunto e o número total dos valores.
MÉDIA ARITMÉTICA PONDERADA
Consideremos uma coleção formada por n números, de forma que cada um esteja sujeito a um peso (valor que indica a quantidade de vezes em que cada número se repete).
A média aritmética ponderada desses n números é a soma dos produtos de cada um por seu peso, dividida pelos somatórios dos seus pesos, isto é:
Nota: “peso” é sinónimo de “ponderação
MODA: (Mo)
É o valor que ocorre com maior frequência.
Quando dois valores ocorrem com a mesma frequência, cada um deles é chamado de uma moda, e o conjunto se diz BIMODAL.
Se mais de dois valores ocorrem com a mesma frequência máxima, cada um deles é uma moda e o conjunto é MULTIMODAL.
Quando nenhum valor é repetido o conjunto não tem moda
MEDIANA (Md)
Valor do meio do conjunto de dados, quando os valores estão dispostos em ordem crescente ou decrescente; divide um conjunto de dados em duas partes iguais.
Para calcular:
- Disponha os valores em ordem (crescente ou decrescente)
- Se o número de valores é ímpar, a mediana é o número localizado no meio da lista.
- Se o número é par, a mediana é a média aritmética dos dois valores do meio.
MEDIDAS DE DISPERSÃO
Existem algumas medidas chamadas medidas de dispersão, que procuram mostrar como os elementos do conjunto se comportam em torno da região central, ou seja, medidas que mostram se eles estão mais ou menos dispersos.
Por exemplo, num jogo de duplas de tênis, são conhecidas as idades dos jogadores:
|
Equipe A |
Equipe B |
| O jogador 1 tem 26 anos; | O jogador 1 tem 45 anos; |
| O jogador 2 tem 24 anos. | O jogador 2 tem 5 anos. |
Veja que, nos dois casos, a média das idades é a mesma, ou seja, 25 anos.
No entanto, as idades da equipe B estão bem mais dispersas em torno da média do que as idades da equipe A.
Duas medidas de dispersão são chamados de Variância e Desvio-Padrão.
VARIÂNCIA
Veja, por exemplo, o conjunto de dados:
2, 5, 6, 8, 14,
Onde a média aritmética é 7. A diferença entre cada valor é a média é chamada desvio. Assim, os desvios para o nosso conjunto de dados serão:
Observação: a soma dos desvios é sempre nula.
Chamamos variância de um conjunto de dados a média aritmética dos quadrados dos desvios. No nosso exemplo, temos:
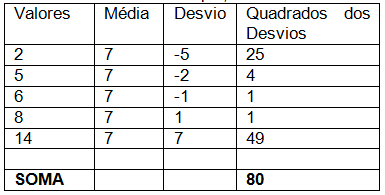
A variância é :
DESVIO-PADRÃO
O desvio-padrão é definido como a raiz quadrada da variância, sendo indicado por
Assim, no nosso exemplo, temos:


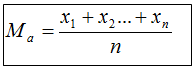
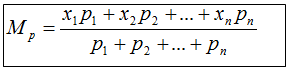


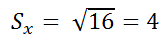

mais se uma moeda lançada 3 vezes sucessivamente .qual e a probabilidade de observamos tipo exatamente uma cara ? ou no maximo 2 caras ?
a probabilidade é 33,3%